Числа и формулы
|
|
|
целые числа Целые числа - это множество натуральных чисел (1, 2, 3, ...), нуля 0 и отрицательных чисел (-1, -2, -3, ...). |
 |
|
деление, делители В формуле y=n/x y-частное, n-делимое, x-делитель. Разложение на простые множители - это представление целого числа в виде произведения простых чисел. Кратное - это число, делящееся на данное целое число х без остатка. Для двух чисел х и у важно их наименьшее общее кратное (НОК). |
 |
|
действительные
числа ... +
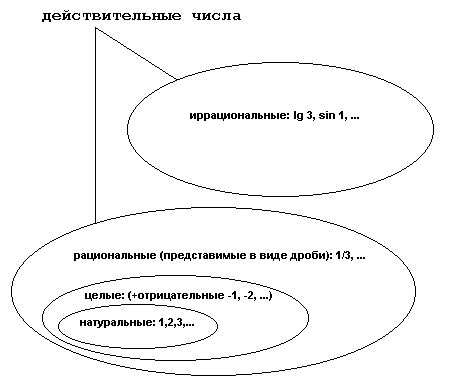
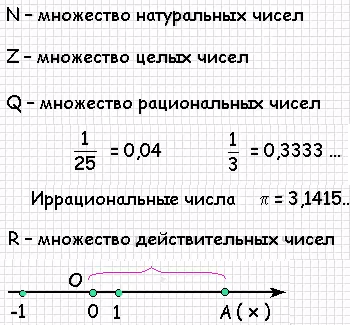
расчет (pdf) Действительные (вещественные) числа - это совокупность чисел рациональных (которые можно представить в виде дроби) и иррациональных (выражающих отношение несопоставимых отрезков, таких, например, как диагональ квадрата и его сторона) |
 |
|
множество Числовое множество - это совокупность чисел, объединенных в группы согласно некоторым общим свойствам. Числовые множества — это множества натуральных, целых, рациональных, вещественных и комплексных чисел вместе с определёнными для соответствующих множеств алгебраическими операциями. |
 |
|
простые и
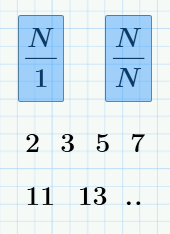
составные числа Простые числа - те, которые делятся только на 1 и на себя. В формуле y=n/x y-частное, n-делимое, x-делитель. Наибольший общий делитель (НОД) чисел N и K – это наибольшее из тех чисел Х, на которые и N, и K делятся нацело. |
 |
|
признаки делимости Существуют несложные правила деления нацело на 2,3,5,9,10. |
 |
|
числовая прямая Числовая ось, или числовая прямая, — это прямая, на которой выбраны: 0.точка 0 — начало отсчёта (ноль); 1.положительное направление, (противоположное направление называется отрицательным); 3.масштаб |
 |
|
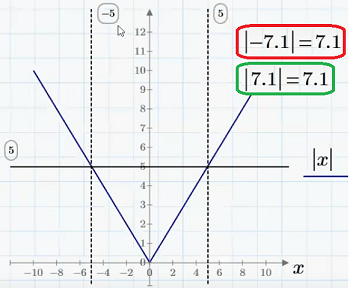
модуль числа Для действительных х: если х неотрицательное, модуль (или абсолютное значение) равен самому числу х; и |x|=-x, если x<0 |
 |
|
переменные,
формулы Те величины, которые сохраняют свое значение неизменным, называются постоянными (или константами). Те, что могут принимать в расчетах разные значения - называют переменными. |
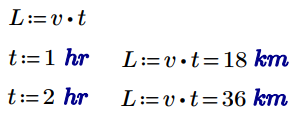 |
|
размерные числа В инженерных и физических расчетах числа могут обладать размерностью, которая выражает их физический смысл и показывает их относительную величину в выбранных единицах измерения |
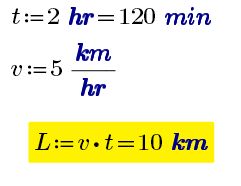 |
|
округление Округлить число до n-го разряда – значит найти его приближение с точностью до единицы n-го разряда (сверху или снизу). Значащая цифра десятичной дроби - это ее первая (слева направо) отличная от нуля цифра, а также все следующие за ней цифры. Округлить число с точностью до n-й значащей цифры – значит округлить его до того разряда, где находится n-я значащая цифра. |
 |
|
пропорция Пропорция - это просто соотношения вида a/b=c/d. Иногда удобнее пользоваться формулой: a∙d=b∙c. |
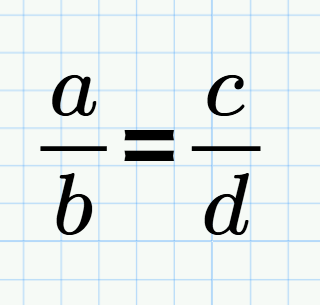 |
|
процент Процент - это 1/100 часть чего-либо. Например, 1% от числа 5000 равен 50, а 30% от 5000 равно 1500. |
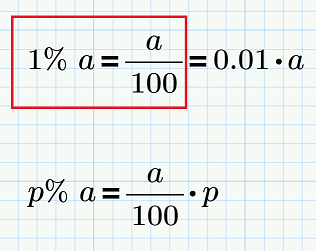 |
|
прямая
пропорциональность Зависимость вида y(x) = a∙x, где a - коэффициент пропорциональности |
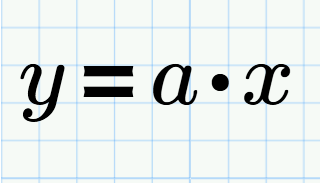 |
|
обратная
пропорциональность Зависимость вида y(x) = a/x, где a - коэффициент пропорциональности |
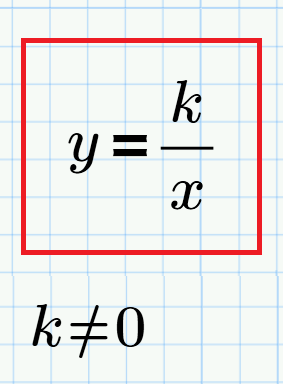 |
|
арифметика: тест тест по арифметике: test1 |
 |
|
комплексные числа Мнимая единица i - это особое гипотетическое число, квадрат которого равен -1; комплексные числа - это числа, получающиеся в результате математических действий над числом i и действительными числами |
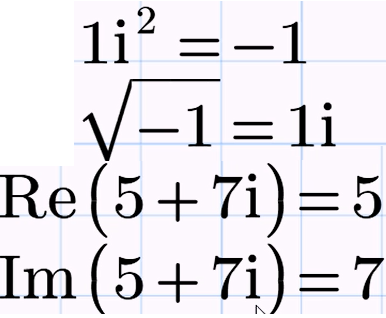 |
|
STEPIK:
элементарная алгебра STEPIK: вводный курс по элементарной алгебре, в котором слушателю предлагается изучить ее на практических примерах, в бесплатном математическом редакторе Mathcad Express (его надо установить до начала работы с курсом). Курс близок по содержанию к знаменитому учебнику по алгебре (начала ХХ века) А.П.Киселева. |
 |
|
Д.Кирьянов:
алгебра Курс по основам предмета элементарная алгебра: числа, формулы, делимость, степени, корни, уравнения, неравенства, пропорции, проценты |
 |